ありきたりな見出しや書き出しは誰にも相手にされない、というのは偽である。私たちは日々ありきたりの文字群に遭遇しているが、その中の幾つかには意味を見出しているからである。そうやって生きている。あけましておめでとうございます。
初詣で面白い絵馬を見つけた。算額とかかれているそれは、昔の人が和算の問題と解答を記し神社に奉納したものである。正月は暇だったので問題を解いてみることにした。問題文はこれ。
今有如団扇面 及作平円三分乃一 内斜容東円
一個与西円及南円北円各二個各充内
無動只伝南円径若干問北円径術如何
よくわかんないけど、写真の図を見ながら現代語に適当に訳してみた。
ここに中心角120度の扇型の図形がある。扇の端点を結んだ斜線の中に東円が一個ある。
そして西円と南円と北円は各二個ずつあって、どれも扇に接しており動かない。この時北円の直径はいくらか。
なるほど!ちょっとわかってきた。まず東円の半径は簡単に求められる。扇の半径をrとすると、r/4だ。つぎに西円をいい感じに計算しよう。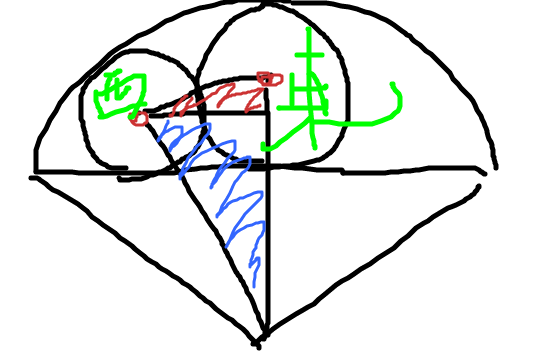
この絵の赤の三角形と青の三角形に注目し、三平方の定理をつかってあれする。そうすると西円の半径は3r/16となる。あとは北円を求めよう。これはデカルトの円定理というのを使う。
デカルトの円定理 - Wikipedia
そうすると北円の半径は 3r(25+2√3)/193となる。やったね。やったけどさ、答えとなんか違うらしいのよ。
術曰置三千零七十二個平方開之加六十二個以百九十三個除之乗南円径
南円の径と比較してどうこう、というふうに答えないといけないみたい。あと、この漢字の羅列がいったいどのような数式になるのかわからない。193は合ってるみたいだけれど。
不完全なまま、この記事を終わりにしよう。今年はとりあえずすべてのアウトプットをブログにつなげるようにしたい。たとえそれが完成していなくても。書きたいことがたくさんあって、はやくやらないと忘れてしまいそうなんだ。
今週のお題「2018年の抱負」
